▶ Plotting

1 Matplotlib

We will be covering key plotting APIs that will be very useful for visualization of machine learning data.

https://medium.com/mlpoint/matplotlib-for-machine-learning-6b5fcd4fbbc7

import matplotlib.pyplot as pl
import numpy as np

#
# an empty figure
#

fig = pl.figure(figsize=(3, 3))
pl.xlabel('X labels go here')
pl.ylabel('Y labels go here')
pl.xticks([0,1,2,3,4,5])

#
# get the axis object to set the tick labels
#
ax = pl.gca()
ax.set_xticklabels(['a', 'b', 'c', 'd', 'e', 'f']);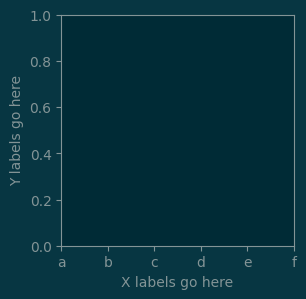

pl.figure(figsize=(6,6))

x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y1 = np.sin(x)
y2 = np.cos(x)

pl.plot(x, y1, color='red', linestyle='-')
pl.plot(x, y2, color='blue', linestyle='--')

pl.legend(['y1=sin(x)', 'y2=cos(x)'], loc='upper right');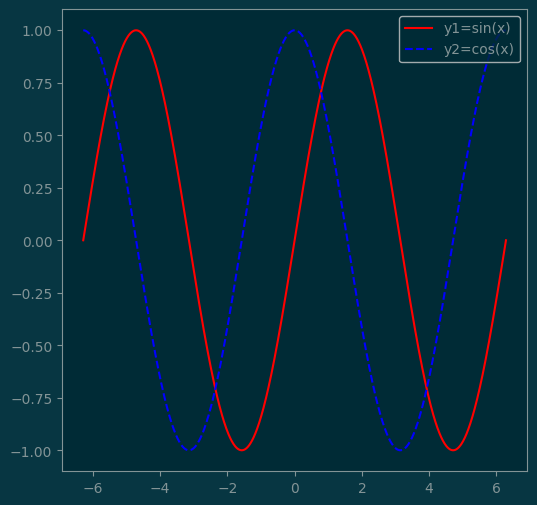

2 Line plots

#
# Plotting line with annotation
#

x = np.linspace(-1, 1, 20)
y1 = np.abs(np.random.randn(20))
pl.plot(x, y1, '-o')

pl.text(x[10], y1[10], 'midpoint', fontsize=12);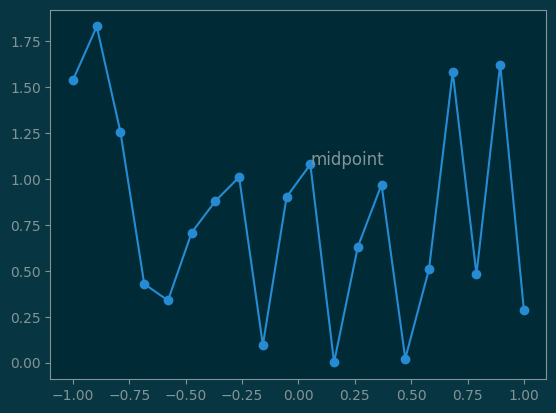

#
# Area plot
#

pl.fill_between(x, y1, color='blue', alpha=0.1)
pl.plot(x, y1, linewidth=2, color='blue');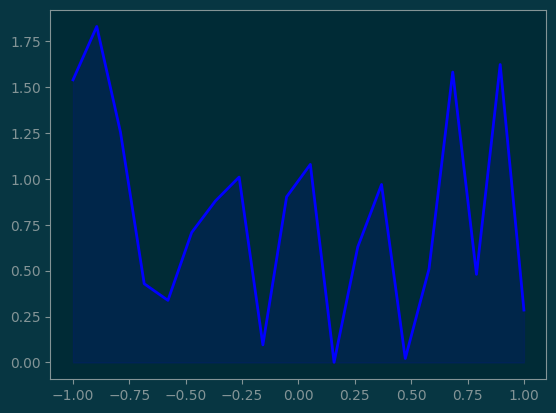

y2 = - y1 / 2

pl.fill_between(x, y1, y2, color='gray', alpha=0.5);
pl.plot(x, y1, x, y2, color='black', linewidth=2);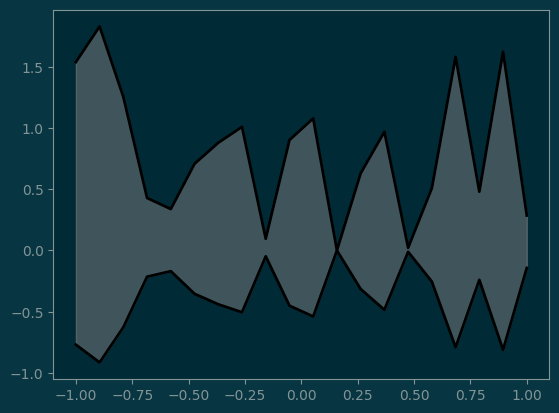

3 Bar Plots

names = ['Jack', 'Jill', 'Joe']
x = np.array([0, 1, 2])
grades = [70, 75, 80]

pl.bar(x, grades)
pl.xticks(x, names);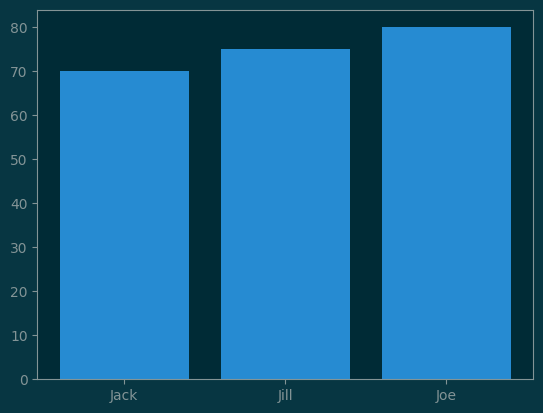

grades_winter = [95, 95, 90]

pl.bar(x+0.00, grades, width=0.25, label='Fall')
pl.bar(x+0.25, grades_winter, width=0.25, label='Winter')
pl.ylim(None, 120)
pl.legend(loc='upper left');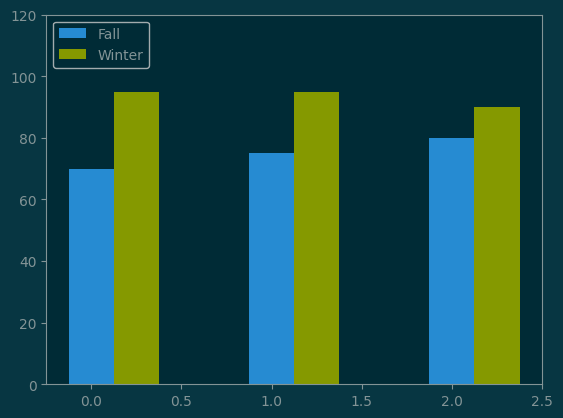

#
# final, midterm, quiz
#

grades = np.array([
    [30, 30, 10],
    [50, 30, 15],
    [45, 23, 5],
])

pl.bar(x, grades[:, 0], label='final')
pl.bar(x, grades[:, 1], bottom=grades[:, 0], label='midterm', )
pl.bar(x, grades[:, 2], bottom=grades[:, :2].sum(axis=1), label='quiz')
pl.legend()
pl.xticks(x, names);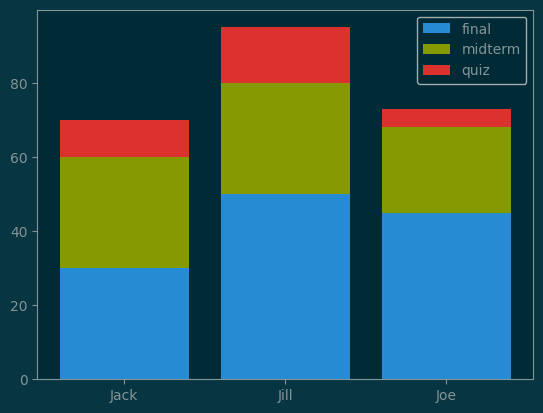

4 Scatter Plots

n = 500
x = np.random.randn(n)
y = np.random.randn(n)
pl.scatter(x, y, s=10);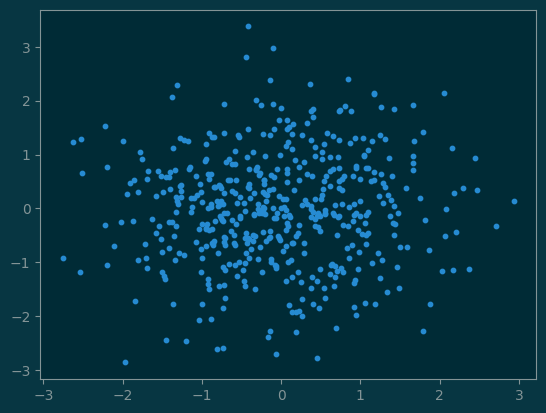

#
# with size variation
#
size = np.abs(np.random.randn(n)) * 30
pl.scatter(x, y, s=size, alpha=0.4, linewidth=0);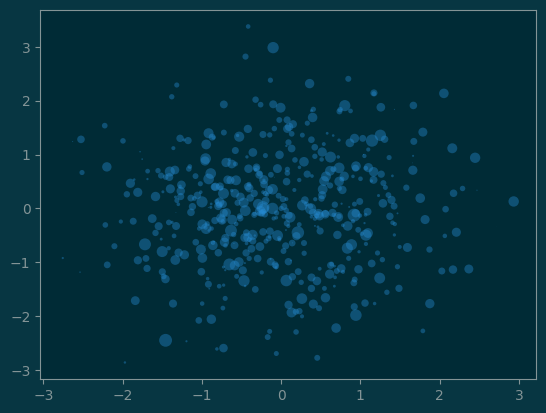

#
# with color variation
#

colors = np.full((n,), '#f00')
colors[x <= y] = '#0f0'

pl.scatter(x, y, s=size, c=colors, alpha=0.4, edgecolors='none');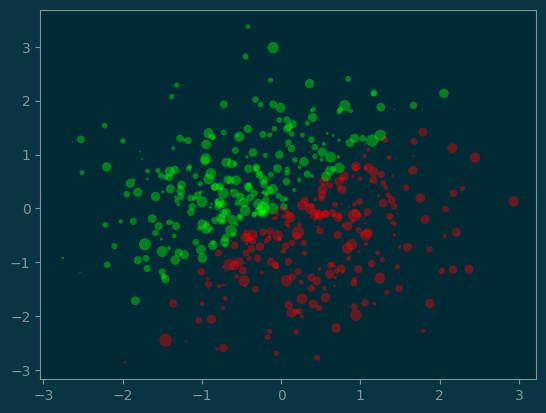

5 More to come

As we proceed further with the topics of machine learning, we will encounter more mathematical objects and ways to show them graphically.

We will look at:

generate meshgrids
contour plots of potential functions
quiver plots for field functions
3D plots for higher dimensional datasets

6 Contours

Suppose we have the following potential function over the 2D space.

\[ z = \sin(\sqrt{x^2 + y^2}) \]

We want to compute the potential function in the region of \([-10, 10]\) by \([-10, 10]\).

xs = np.linspace(-10, 10, 100)
ys = np.linspace(-10, 10, 100)
zs = np.zeros((100, 100))

Warning

Do not use loop.

#
#  You should not be doing this.
#

for i in range(xs.size):
    for j in range(ys.size):
        zs[i,j] = np.sin(np.sqrt(xs[i]**2 + ys[j]**2))

zs.shape

(100, 100)

Note

The proper way is to use meshgrid.

X, Y = np.meshgrid(xs, ys)
X.shape, Y.shape

((100, 100), (100, 100))

Z = np.sin(np.sqrt(X**2 + Y**2))
Z.shape

(100, 100)

pl.contour(X, Y, Z, levels=15, cmap='gray')

<matplotlib.contour.QuadContourSet at 0x7ff4e1f9b820>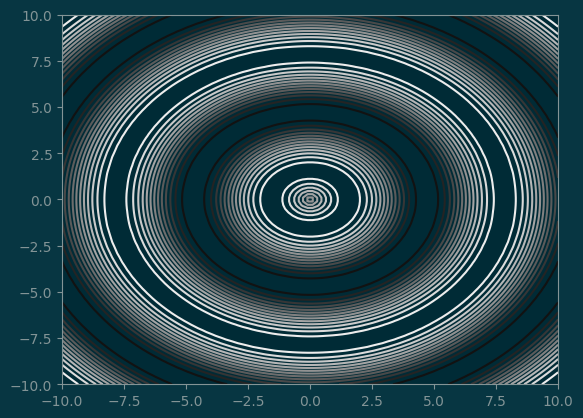

pl.contourf(X, Y, Z, levels=15, cmap='jet');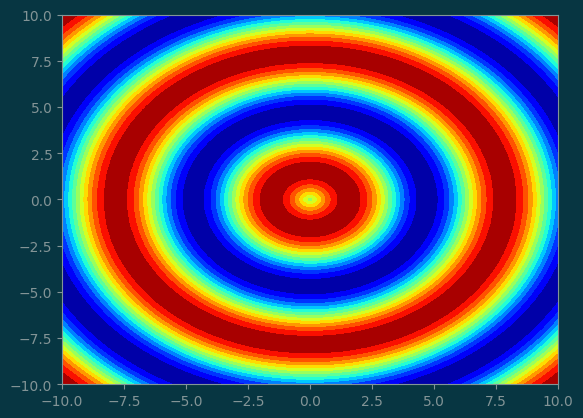

pl.contourf(X, Y, Z, levels=[np.min(Z), np.mean(Z), np.max(Z)], cmap='jet');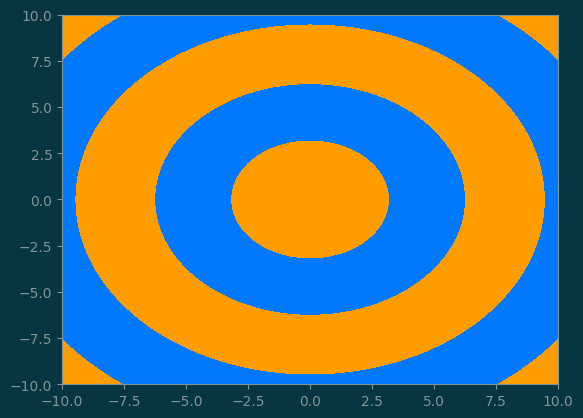

7 Vector fields

X, Y = np.meshgrid(
    np.linspace(-5, 5, 10),
    np.linspace(-5, 5, 10)
)

u = 1
v = -1

pl.quiver(X, Y, u, v, color='white');

u = X
v = Y

pl.quiver(X, Y, u, v, color='white');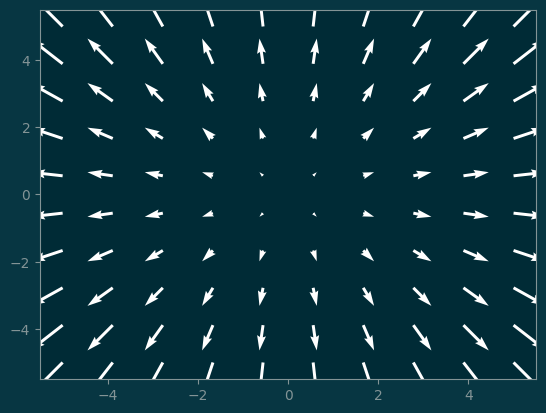

Here is a call vector field:

\[ \vec F(x, y) = -\frac{y}{\sqrt{x^2+y^2}}\mathbf{i} + \frac{x}{\sqrt{x^2+y^2}}\mathbf{j} \]

u = -Y / np.sqrt(X**2 + Y**2)
v = X / np.sqrt(X**2 + Y**2)

pl.quiver(X, Y, u, v, color='white');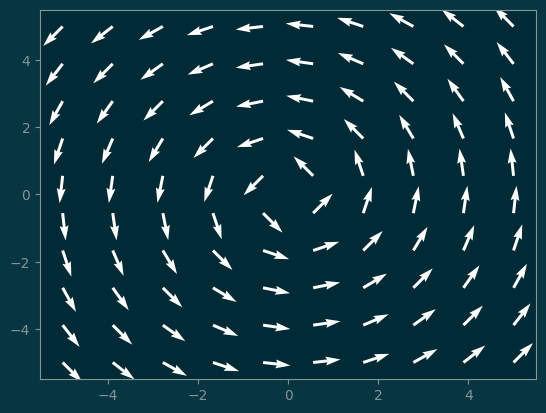

8 3D plot points and lines

from mpl_toolkits import mplot3d

fig = pl.figure()
ax = pl.axes(projection='3d')

ax = pl.axes(projection='3d')

zs = np.linspace(0, 15, 1000)
xs = np.sin(zs)
ys = np.cos(zs)

ax.plot3D(xs, ys, zs, linewidth=2, color='red');

z2 = np.random.random(100) * 15
x2 = np.sin(z2) + 0.1 * np.random.random(100)
y2 = np.cos(z2) + 0.1 * np.random.random(100)
ax.scatter(x2, y2, z2, c=z2, cmap='jet');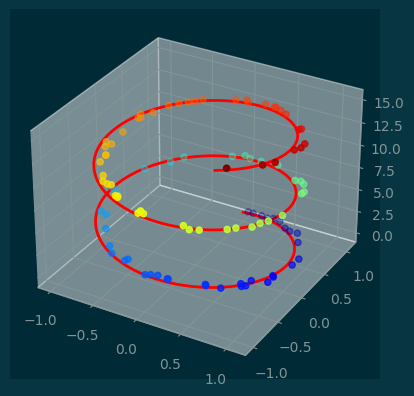

9 3D Contours

xs = np.linspace(-6, 6, 30)
ys = np.linspace(-6, 6, 30)

X, Y = np.meshgrid(xs, ys)
Z = np.sin(np.sqrt(X ** 2 + Y ** 2))

X.shape, Y.shape, Z.shape

((30, 30), (30, 30), (30, 30))

ax = pl.axes(projection='3d')
ax.contour3D(X, Y, Z, levels=100, cmap='jet')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');

## ax.view_init(60, 35);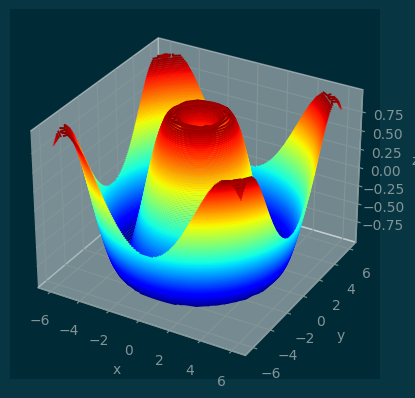

#
#
#